Пусть задан набор из m эталонов — n- мерных векторов xi . Требуется построить сеть, которая при предъявлении на вход произвольного образа — вектора x — давала бы на выходе «наиболее похожий» эталон.

Всюду далее образы и, в том числе, эталоны — n- мерные векторы с координатами ±1. Примером понятия эталона «наиболее похожего» на x может служить ближайший к x вектор xi. Легко заметить, что это требование эквивалентно требованию максимальности скалярного произведения векторов x и xi :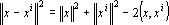

Первые два слагаемых в правой части совпадают для любых образов x и xi , так как длины всех векторов-образов равны √n. Таким образом, задача поиска ближайшего образа сводится к поиску образа, скалярное произведение с которым максимально. Этот простой факт приводит к тому, что сравнивать придется линейные функции от образов, тогда как расстояние является квадратичной функцией.