Формальная постановка задачи
Рассмотрим множество из m объектов x , каждый из которых является n- мерным вектором с действительными координатами (в случае комплексных координат особых трудностей с данным методом также не возникает, но формулы становятся более сложными, а комплексные значения признаков случаются редко).
Зададим пространство ядер классов E , и меру близости dist(a, x) , где a — точка из пространства ядер, а x — точка из пространства объектов. Тогда для заданного числа классов k необходимо подобрать k ядер таким образом, чтобы суммарная мера близости была минимальной. Суммарная мера близости записывается в следующем виде: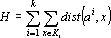 
(1)
где Ki — множество объектов i —го класса.
Другое по теме
2. Скалигер и Петавиус. Создание в XVI–XVII веках общепринятой ныне
версии хронологии и истории древности и Средневековья
Хронология древней и средневековой истории в том виде, в
каком мы имеем ее сейчас, создана и в значительной мере завершена в серии
фундаментальных трудов XVI–XVII веков, начинающейся трудами ИОСИФА СКАЛИГЕРА
(1540–1609) (Ioseph ...