Цель доказательства — убедиться в том, что теорема Пифагора верна для всех прямоугольных треугольников. Треугольник, изображенный на рисунке слева, может быть любым прямоугольным треугольником, так как длины его сторон не указаны, а обозначены буквами x, y и z . Справа из четырех одинаковых прямоугольных треугольников и наклоненного квадрата составлен квадрат больших размеров. Площадь большего квадрата — ключ к доказательству.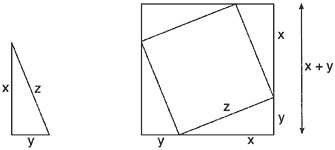

Площадь большого квадрата можно вычислить двумя способами.

1-й способ. Измеряем площадь большого квадрата как единой фигуры. Длина каждой стороны равна x +y . Следовательно, площадь большого квадрата равна (x +y )2.

2-й способ. Измеряем площадь каждого элемента большого квадрата. Площадь каждого треугольника равна xy /2. Площадь наклонного квадрата равна z 2. Следовательно, площадь большого квадрата равна 4 × (площадь каждого треугольника) + (площадь наклонного квадрата) = 4·xy /2 + z 2. 1-й и 2-й способы приводят к двум различным выражениям. Оба выражения должны быть равны, так как они представляют различные записи одной и той же площади. Следовательно,

(x + y)2 = 4·xy/2 + z2

.

Раскроем скобки и упростим полученные выражения:

x2 + 2xy + y2 = 2xy + z2

.

Члены 2xy , стоящие в левой и правой частях равенства, взаимно уничтожаются, и мы получаем

x2 + y2 = z2

.

Это и есть теорема Пифагора!

Приведенное доказательство остается в силе для любых прямоугольных треугольников. Длины сторон треугольника в нашем доказательстве обозначены буквами x, y и z , которые могут быть длинами сторон любого прямоугольного треугольника.