4. Взаимное расположение двух прямыхСтраница 2
Прямые будут являться скрещивающимися, если они не параллельны и не пересекаются. Это вытекает из того, что возможны только три случая взаимного расположения прямых.
Для скрещивающихся прямых справедливы утверждения:
1) точки пересечения одноименных проекций на горизонтальной и фронтальной плоскостях не лежат на одном перпендикуляре к оси х (прямые I и II на рис. 31).
2) хотя бы в одной паре одноименные проекции не параллельны (прямые III и IV на рис. 31).
Рисунок 31 показывает проекции четырех прямых, любая пара из которых скрещивается.
Как и в рассмотренных ранее случаях, обратное утверждение для скрещивающихся прямых несправедливо при условии, что хотя бы одна из прямых является профильной. 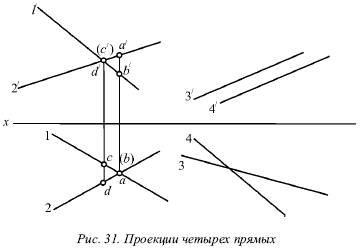
Другое по теме
Вычислительный эксперимент и задачи
Задачи оптимального управления относятся к теории экстремальных задач, то есть задач определения максимальных и минимальных значений. Уже то обстоятельство, что в этой фразе встретилось несколько латинских слов (maximum на ...